Several of our classes involve students using mathematical expressions, but there was no way for us to automatically check this work. The stated solution to a problem may be x+y, but if a student answers y+x, our system needs to understand that this is also correct. This equivalence should not be limited to simply associativity and commutativity; expressions like 1-cos^2(x) should also be accepted in place of sin^2(x).
For the solution, we considered a number of factors: how the language or framework we chose would integrate into our system, how much we could customize this solution (in order to fix bugs or add additional capabilities), and the solution’s fit for our problem. While building an equivalence checker from scratch would have given us the greatest flexibility and control over our tool, this would have been an inefficient use of engineering effort – the problem of algebraic manipulation and equivalence checking has already been deeply explored by systems such as Wolfram Alpha, Mathematica, Maple TA, WeBWorK, and SageMath.
There are two primary approaches to equivalence checking: symbolic and numeric. Symbolic systems seek to use a series of transformation rules to prove two expressions equal, while numeric systems verify equivalence by substituting values for variables and checking that the resulting expressions evaluate to approximately the same value. While symbolic systems may be more “correct,” since they won’t suffer from numeric error, checking equivalence symbolically also tends to be more time-consuming, and runs the risk of being unable to resolve two expressions that are in fact equal, if the system’s transformation rules are not sufficient. On the other hand, the primary drawback of numeric systems is that only a finite number of variable values can be sampled, which may cause the system to conclude to expressions are equal if it does not sample any points for which the expressions differ.
Ultimately, our goal is to provide the best learning experience for students. In doing so, we certainly do not want to mark a correct solution as wrong; it is less important to prevent solutions that deliberately attempt to circumvent the numeric system, for example x^2+0.00000000000000001 in place of x^2. Because of this, we have decided to leverage sympy , an open source Python library for symbolic mathematics that is also used by SageMath, by using the parser it provides and running basic symbolic checking. If the symbolic check succeeds, we can state with confidence that the student’s solution is correct, but if it fails, we continue to a numeric check. Sympy also has the ability to generate LaTeX code for math expressions, allowing a student to sanity check an answer by previewing it before submitting:
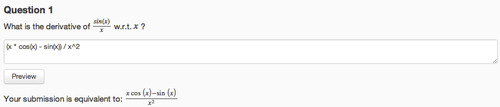
Expression checking will be used by Bioelectricity: A Quantitative Approach (starting today, September 24th!) and Calculus: Single Variable (starting January 7th, 2013).
I hope you enjoy this new feature!
–Colleen Lee, Software Engineer
